Link to the FireBridge substack article
In general, the slope of a hill or incline is often determined to be the ratio between the vertical distance, to that of the horizontal distance. Any number of terms can be used by the individual to reference this but the most commonly used term is Rise over Run.
The image below shows a generalized version of a simulated slope of a hose lay that is to be run up a slope of a hill.
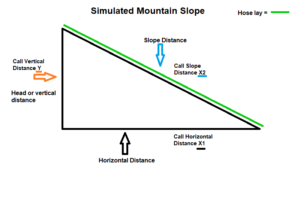
We can see we have identifiers for our horizontal, vertical, and slope or diagonal distances.
These are: Vertical = Y, Horizontal = X1, Slope Distance = X2. In standard math, we would determine our slope percent by taking the Y and dividing by the X1. This initial result would be the number we would use for the slope ratio.
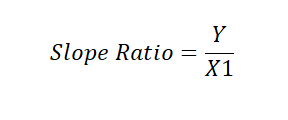
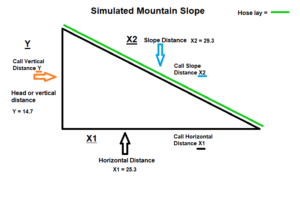
If you were to measure out a triangle with a rule and make the triangle as that shown above with the following dimensions you would obtain the following slope ratio.
X2 = 29.3cm, X1 = 25.3cm, and Y = 14.7cm
Here is the image again:

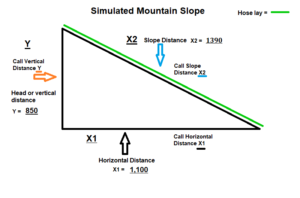
In the forest when setting up a hose lay, we do not see the X1 component, because we are laying out the hose on the X2 portion. By dividing the would give us a ratio that would be for the wrong side. There is a way to figure this out though.
Take the Vertical of Y and Divide by the X2 for the slope distance: this will give you a figure of .502. Now to obtain the horizontal distance of X1, multiply that Ratio by 100 and then multiply that figure by the ratio we first obtained.
Then multiply the 50.2 by the original slope ratio to obtain the X1 distance. . This 25.2 is the actual Horizontal Distance of X1. To see the effect this will have, now you can redo the slope ratio formula to obtain the true number for the slope.
There is also another way to determine distances.

Once you know this, you can use this slope ratio to not only determine slope rate in percent, you can determine distances that your pump can deliver water to. For example, we have a Mark 3 pump that we need to move 20 gallons per minute. The issue is we only have 320 psi to work with and out of this we need to provide Friction Loss, Nozzle Pressure, and Head Pressure. So how can we use slope ratios to determine distances we can pump? We must first subtract from this maximum pressure any constant pressures that we cannot leave out. This is our Friction Loss and Nozzle Pressure.
Figuring 100 psi for Np, and then Fl for 20gpm is 1.4 per 100 feet so 1.4 x 11 = 15.4. Add the two figures together and we have 115.4psi. At this point, you must subtract this figure from the Pumps Max psi for that flow which is 320psi.
This is the pressure that you have to work with to determine the maximum elevation you can reach. First, we have to determine what this 204.6 psi equates to in elevation. This step requires we take the 204.6 and divide it by .434(the psi to raise water 1 foot).
(review the pdf to see the rest of this information)

Comments